Drops: Calculating landing force

A mechanical engineer wants to know how I calculated the impact forces for a bike drop. Yikes, here goes …

Greetings! I’ve been really enjoying your site. I’m working on getting a 2005 Enduro, and whilst doing a search at lunchtime came upon your fine pages. I’ve enjoyed reading reports of rides you’ve done in places I’ve been, especially Moab (Porcupine Rim and Slickrock, ridden on a ’97 Schwinn Homegrown FS), and your dirt biking article was great, too. I had the chance to take my XR600 to a 24 Hours of Moab race a few years back, and rode lots of great trails in the Behind-the-Rocks area while waiting for my friends to ride themselves sick.

What really got my attention was your article on doing drops. For my senior project in getting a mechanical engineering degree, I had to chance to work with Chris Titus (actually, a guy named Travis, their drafter) on doing some FEA and analysis on what was then their new DH bike, the SuperMoto. They wanted to know what would happen if a 200 pound rider landed on the seat from a 5 foot drop. To come up with some sort of realistic answer I first created a solid model of the frame using a program called Pro/Engineer, then subjected it to various stresses to see how it would react. I also did a lot of calculations and computer programming to figure out the effect of frame stiffness, spring deflection, and shock absorber effect on how much absorption took place, versus shock transmitted to the rider. What I found out is that this is a VERY complex system, with a lot of variables that have a marked effect on the answers I got.

When I saw your graph, it kind of gave me a start, because it looked very much like some of the graphs I came up with, after a LOT of work and calculations using second order differential equations to model the shock absorber. I’m very curious about how you came up your graph, and would love it if you could share your methods with me. I finally finished the project (I could email you a copy, if you were REALLY interested) and graduated, but I’m still curious about the subject. There was a lot more I could have done, and someday would like to.

So any thoughts you may have on the subject would be most welcome, and especially any technical info you could share!

Thanks again for a great site!

Tim Gates

Burlington, WA

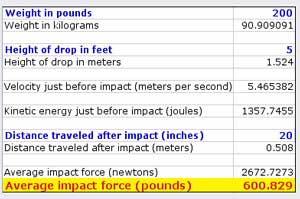Download this nifty Excel calculator.

Hey Tim.

Dude, I’m a liberal arts major — I’ve never even heard of a second order differential equation!

Sounds like you were interested in the amount of force and how it interacted with different parts of the bike. I just wanted to calculate the total force and see how different styles of landing (stiff or loose) affect the average impact force. As I found, it’s far better to absorb the impact than to stiff-arm it.

I stuck with the basics:

1. You get the impact velocity (v) from the starting height (h) and the rate of acceleration due to gravity (g), which as you know is 9.8 meters per second squared.

2. You get the total kinetic energy (KE) from the impact velocity (v) and the mass of the object (m). That gives you the total amount of energy going into the landing.

3. To figure out the average impact force (IF), you divide the kinetic energy (KE) by the distance traveled after impact (d).

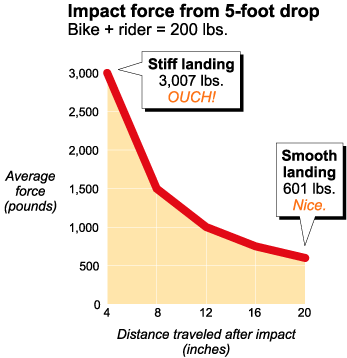
If you land stiffly, all of the impact energy gets expressed at once — ouch! If you use your arms, legs and suspension, that energy gets spread over time, and the forces are greatly reduced. In my simulation of the 200-pound rider dropping five feet, the stiff landing created 3,000 pounds of force, while the smooth landing yielded only 600 pounds. That’s a big difference! Here’s the story.

I made an Excel calculator that’s really easy to use. Download it here. Yes, nerd style!

Tim, I know this is really simple, but I hope it makes sense to you. Thanks for the props, and keep calculating!

— Lee

I learned a lot from the HyperPhysics site.